Math makes me like a wrecking ball: Dimensi 3 Bangun Ruang

Rumus Bangun Ruang – Ciri khusus dari bangun ruang adalah terletak pada bentuknya yang terlihat 3 dimensi yang secara grafiknya yakni x, y dan z). Berbeda dengan bangun datar yang berbentuk 2 dimensi dan tidak mempunyai ruang. Nah, bagi anda yang ingin mempelajari bangun ruang, pada artikel ini kita akan mencoba membahasnya dengan lebih lengkap.
Seperti yang dijelaskan di atas bahwa bangun ruang ciri utamanya ialah memiliki ruang dan atau volume. Bangun ruang sendiri memiliki berbagai macam bentuk, yakni balok, kubus, kerucut, prisma, tabung, bola dan limas. Setiap bangun ruang tersebut memilikiperhitungan yang berbeda-beda ketika anda akan mencari luas dan juga volumenya.

Rumus Bangun Ruang Lengkap

1. Rumus dan Ciri Balok

Balok merupakan sebuah bangun ruang yang memiliki 6 bidang yang memiliki bentuk persegi panjang. Berikut adalah beberapa ketentuan atau ciri-ciri balok.

Memiliki 6 buah sisi dan berbentuk 4 persegi panjang
Memiliki 12 rusuk, yang dibagi menjadi 3 kelompok, setiap kelompok terdiri atas 4 buah rusuk yang memiliki panjang yang sama.
Luas sisi yang berhadapan adalah sama, sisi-sisi tersebut terdiri dari 3 bagian yang saling berhadapan
Semuanya sudutnya siku-siku atau memiliki nilai90⁰

Rumus Perhitungan Balok

Volume Balok

V = p x l x t

Luas Permukaan Balok

L = 2 x { ( p x l ) + ( p x t ) + ( l x t ) }

Keliling Balok

K = 4 x (p + l + t)

Keterangan:

p = panjang
l= lebar
t = tinggi

2. Rumus dan Ciri Kubus

Kubus adalah bangun ruang yang terdiri atas 6 sisi yang mempunyai bentuk bujur sangkar. Ciri-ciri kubus adalah sebagai berikut.

Memiliki 6 sisi yang memiliki luas yang sama
Bentuknya persegi
Memiliki 12 rusuk yang memiliki panjang yang sama
Setiap sudutnya siku-siku (90^⁰

Rumus Perhitungan Kubus

Rumus Volume Kubus

V = s x s x s = a³

Luas Permukaan Kubus

L Permukaan = 6 x s x s = 6 x s²

Keliling kubus

K = 12 x s

Keterangan :
s = panjang rusuk atau sisi kubus

3. Rumus dan Ciri Bola

Tentunya anda sudah tidak asing lagi dengan bangun ruang bola ini. Berikut beberapa ketentuan bangun ruang dinamakan bola.

Bundar dan merata kesemua arah
Memiliki jari-jari yang sama panjangnya dari titip tengah (titik pusat) ke semua arah
Apabila dibelah menjadi dua yang mana melewati titik pusat maka memiliki garis tengah 2 x panjang jari-jari

Rumus Perhitungan Bola

Volume Bola

V = 4/3 x π x r³

Luas Permukaan

L = 4 x π x r²

Keterangan :

r = jari-jari
π = 22/7 atau 3,14

4. Rumus dan Ciri Limas

Bangun ruang ini juga terdiri atas berbagai macam bentuk. Perbedaan yang sangat mencolok dari bentuk satu dengan yang lainnya adalah terletak pada alasnya, ada yang mempunyai alas segi lima, segi empat dan juga segitiga dan masih banyak lagi. Namun alas limas ini hanya memiliki sifat segi tidak berebntuk bundar. Jika alasnya berbentuk bundar maka disebut dengan nama kerucut.
Rumus Perhitungan Limas Segiempat

Luas Alas

L a = sisi x sisi

Luas Sisi Δ

Luas Sisi Δ = 1/2 x a x t

Volume :

V = 1/3 x L alas x t

Luas Permukaan Limas

LP = { ( p + l ) x t) + ( p x l )

5. Rumus dan Ciri Tabung

Seperti halnya bola, tabung ini juga sudah tidak asing lagi, seringkali kita liat dalam kehidupan sehari-hari. Seperti drum, kaleng dan lain sebagainya. Tabung ini mempunyai alas dan juga atas yang mana bentuknya adalah lingkaran. Nah berikut rumus perhitungannya

Rumus Tabung

Luas Alas
L = π x r²
Karena bentuknya seperti lingkaran baca juga artikel sebelumnya mengenai luas lingkaran.
Luas selimut
L = 2 x π x r x t
Luas Permukaan
L = 2 x L alas + L selimut = 2 x π x r²+ 2 x π x r x t = 2 x π x r x ( r x t )
Volume Limas Segi Empat
V = π x r² x t

6. Rumus dan Ciri Kerucut

Seperti layaknya tabung, kerucut juga memiliki alas yang berbentuk lingkaran namun kerucut tidak memiliki penutup atas. Berikut ini adalah rumus bangun ruang kerucut.

Rumus Perhitungan Kerucut

Luas selimut
L = π x r x s
Luas Alas
L alas = π x r²
Luas Permukaan Kerucut
L = L Alas + L Selimut = π x r²+ π x r x s = π r (r + s)
Volume Kerucut
V =1/3 x L alas x Tinggi = 1/3 x π x r² x t

7. Rumus dan Ciri Prisma Tegak Segitiga

Kubus yang memiliki penutup atas dan bawah segi empat, tabung yang memiliki penutup lingkaran, nah beda lagi dengan prisma dia memiliki penutup segitiga. Macam-macam aja ya! namun itulah uniknya bangun ruang.

Rumus Perhitungan Prisma

Luas permukaan
L = 2 x Luas Alas + Keliling Alas x t
Volume Prisma
V = Luas alas x t

Materi Dimensi Tiga mencakup tentang jarak, sudut pada bangun ruang.
Untuk itulah kita wajib tau tiap bangun ruang . Target kita yang pertama adalah Kubus . Pasti dengar namanya saja udah bisa membayangkan bentuknya kan…???!!
Nah, mari kita kupas tentang sifat-sifat si Kubus ini !

KUBUS ABCD.EFGH

Dalam kubus ABCD.EFGH terdapat :

12 rusuk contoh AB
12 diagonal sisi / diagonal bidang contoh EG
6 bidang / sisi contoh CDHG
6 bidang diagonal contoh ACGE
4 diagonal ruang contoh AG

Yuuuk kita cari rumus diagonal sisi dan diagonal ruang pada kubus ABCD.EFGH dulu yuuuuuuuuuk….

kita akan cari diagonal sisi AC, perhatikan bidang ABCD (persegi)

$\begin{align*}AC&=&\sqrt{AB^2+BC^2}\\&=&\sqrt{r^2+r^2}\\&=&\sqrt{2r^2}\\&=&r\sqrt 2\end{align}$

kita akan cari diagonal ruang AG, perhatikan bidang diagonal ACGE (persegi panjang)

$\begin{align*}AG&=&\sqrt{AC^2+CG^2}\\&=&\sqrt{(r\sqrt 2)^2+r^2}\\&=&\sqrt{2r^2+r^2}\\&=&\sqrt{3r^2}\\&=&r\sqrt 3\end{align}$

Kita rangkum Rumus Kubus dengan rusuk = r

diagonal sisi kubus = $r\sqrt 2$
diagonal ruang kubus = $r\sqrt 3$
Luas permukaan kubus = $6.r^2$
Volume kubus = $r^3$

Contoh soal :
1. Jika diketahui kubus dengan diagonal sisinya $2\sqrt 6$ cm , tentukan diagonal ruang kubus !

jawab :

pertama kita cari rusuk nya dulu ya,

$\begin{align*}diag.sisi&=&2\sqrt 6\\r\sqrt 2&=&2\sqrt 6\\r&=&\frac{2\sqrt 6}{\sqrt 2}\\r&=&2\sqrt 3 \end{align*}$

maka diagonal ruang kubus

$\begin{align*}diag.ruang&=&{\color{Red} r}\sqrt 3\\&=&({\color{Red} 2\sqrt 3})\sqrt 3\\&=&2.3\\&=&6 \end{align*}$

2. Jika diketahui kubus ABCD.EFGH dengan rusuk 5 cm, tentukan luas BDHF !

jawab :

perhatikan BDHF (bidang diagonal) dengan BF = 5 cm (rusuk) dan BD = 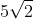$5\sqrt 2$ cm (diagonal sisi)

maka luas BDHF

$\begin{align*}L_{BDHF}&=&BD\times BF\\&=&5\sqrt 2\times 5\\&=&25\sqrt 2\;\;cm^2\end{align*}$

3. Jika diketahui kubus dengan diagonal sisi 6 cm, tentukan Volume kubus tersebut !

jawab :

pertama kita cari rusuknya ya..
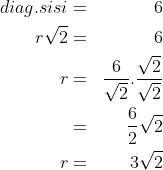
$\begin{align*}diag.sisi&=&6\\r\sqrt 2&=&6\\r&=&\frac{6}{\sqrt 2}.\frac{\sqrt 2}{\sqrt 2}\\&=&\frac{6}{2}\sqrt 2\\r&=&3\sqrt 2\end{align*}$

maka volume kubus

$\begin{align*}V&=&r^3\\&=&(3\sqrt 2)^3\\&=&27.2\sqrt 2\\&=&54\sqrt 2\;\;cm^3\end{align*}$

Sekarang kita masuk ke contoh soal yang berkaitan dengan jarak dan sudut pada bangun ruang…..yuk

Latihan soal bangun ruang yang berkaitan dengan jarak dan sudut

1. Pada kubus ABCD.EFGH dengan rusuk 4 cm, tentukan jarak titik B ke garis EG !

jawab :

titik B dan garis EG berada dalam satu bidang yaitu segitiga BEG(sama sisi)
perhatikan bahwa BE , BG dan EG adalah diagonal sisi sehingga BE = BG = EG = $4\sqrt 2$ cm
proyeksi titik B di garis EG adalah titik P (di tengah EG) sehingga GP = $2\sqrt 2$ cm
jarak yang akan kita cari adalah panjang garis BP

maka :

$\begin{align*}BP&=&\sqrt{BG^2-GP^2}\\&=&\sqrt{(4\sqrt 2)^2-(2\sqrt 2)^2}\\&=&\sqrt {32-8}\\&=&\sqrt{24}\\&=&2\sqrt 6 \end{align*}$

2. Pada kubus ABCD.EFGH tentukan jarak titik A ke garis CE !

jawab :

titik A dan garis EC berada dalam satu bidang yaitu segitiga AEC
perhatikan bahwa AE adalah rusuk, kita misalkan AE = r , sedangkan AC adalah diagonal sisi maka kita misalkan AC = $r\sqrt 2$
proyeksi titik A di garis EC adalah titik Q ( AQ tegak lurus EC)
jarak yang akan kita cari adalah panjang garis AQ

perhatikan segitiga AQE dan segitiga CAE kita gunakan perbandingan sisi

$\begin{align*}\frac{AQ}{AE}&=&\frac{AC}{CE}\end{align*}$