1. Tahukah Anda? Ternyata Nama yang Paling Banyak Diguna di Dunia adalah “Muhammad” disusuli dengan nama “Jack”
2. Albania merupakan negara satu-satunya di benua Eropa yang 90% penduduknya beragama Islam
3. Perkataan-perkataan berikut ini adalah berasal dari bahasa Arab :
Algebra, Zero, Cotton, Sofa, Rice, Candy, Safron, Balcony, bahkan
`Alcohol’ juga berasal dari bahasa Arab, Al-Kuhl, yang mempunyai erti
“bubuk” yang kemudiannya diserap ke dalam bahasa Inggeris.
4.
Beberapa ayat di dalam Al-Qur’an menggambarkan pentingnya persamaan hak
antara lelaki dan wanita (secara perhitungan matematik). Kata “Lelaki”
dan “Wanita” di dalam Al-Qur’an sama-sama berjumlah 24.
5. Islam
merupakan agama yang pertumbuhannya paling cepat di dunia menurut banyak
sumber, dijangkakan akan menjadi agama nombor 1 di dunia pada tahun
2030.
6. Jikalau sekarang Al-Qur’an dihancurkan, maka versi arab
dari Al-Qur’an akan segera direcover oleh jutaan muslim, yang disebut
“Huffaz” yang telah menghafalkan kata-kata di dalam Al-Qur’an dari mulai
awal sampai dengan akhir ayat.
7. Pemeluk Islam bertambah 2,9%
per tahun. Pertumbuhan ini lebih cepat dibandingkan dengan pertumbuhan
jumlah penduduk bumi sendiri yang hanya 2,3% per tahun.
8.
Berdasarkan data dari Kementerian Pertahanan Amerika Syarikat.
Dianggarkan seramai 15,000 orang yang beragama Islam berkhidmat dalam US
Militari ( Stats 1997).
9. Seramai 8 juta orang Muslim yang kini ada di AS dan 20.000 orang AS masuk Islam setiap tahun setelah peristiwa 9/11.
10. Jasad Nabi Muhammad pernah ingin dicuri 2 kali, namun kedua2nya
gagal dan salah satu yang mencuri dihilangkan oleh Allah dari bumi
11. Al Qur’an adalah satu-satunya kitab suci yang boleh dihafal jutaan
manusia (Hafidz/penghafal Al Qur’an) sehingga keaslian/kesuciannya
selalu terjaga.
12. Jika agama lain mempunyai lebih dari 4 versi
kitab suci yang berbeda satu dengan lainnya, maka Al Qur’an hanya ada
satu dan tak ada pertentangan di dalamnya:
13. Para astronaut
telah menemukan bahawa planet Bumi itu mengeluarkan semacam radiasi yang
berpusat di kota Mekah, tepatnya berasal dari Ka’Bah. Yang mengejutkan
adalah radiasi tersebut bersifat infiniti (tidak berakhir), radiasi
tersebut menembus planet mars dan masih berlanjutan. Peneliti
mempercayai bahawa radiasi ini memiliki karakteristik dan menghubungkan
antara Ka’Bah di di planet Bumi dengan Ka’bah di alam akhirat.
14. Kata-kata terakhir Nabi Muhammad sebelum wafat adalah “Ummatii …
ummatii …ummatii” yang mengungkapkan betapa besar cinta Baginda kepada
umatnya.
15. Solat yang pertama dilakukan oleh Rasulallah Saw
menghadap Masjidil Haram adalah solat Asar bersama para sahabat, setelah
sebelumnya berkiblat ke Masjidil Baitul Maqdis selama 16 bulan.
16. Sebanyak 23 kali perang semasa Rasulullah memimpin, hanya sekali
kekalahan yang di derita kaum muslimin, yakni, perang uhud.
17.
Musa A.S adalah nama yang paling sering disebut dalam Al-Qur’an,
sedangkan Maryam adalah satu2nya nama perempuan yang disebut dalam
Al-Qur’an.
18. Semua anak Nabi Muhammad, yakni, Al-Qasim,Abdullah
dan Ibrahim, meninggal kurang lebih pada usia 2 tahun. Allah sengaja
memanggil mereka lebih awal agar kaum muslimin tidak mengangkat mereka
menjadi rasul yang baru.
19. Hajar Aswad itu diturunkan dari
syurga, warnanya lebih putih daripada susu, dan dosa-dosa anak cucu
Adamlah yang menjadikannya hitam.
20. Al Khawarizmi (matematik),
Jabir Ibn Hayyan (kimia), Ibnu Khaldun (sosiologi dan sejarah), Ibnu
Sina (kedoktoran), Ar Razi (kedoktoran), Al Biruni (fizik), Ibnu Batutah
(antropologi) adalah contoh dari ratusan cendikiawan muslim yang
menjadi rujukan dalam ilmu pengetahuan moden.
Math makes me like a wrecking ball
Rabu, 28 Mei 2014
Dimensi 3 Bangun Ruang
Rumus Bangun Ruang
– Ciri khusus dari bangun ruang adalah terletak pada bentuknya yang
terlihat 3 dimensi yang secara grafiknya yakni x, y dan z). Berbeda
dengan bangun datar yang berbentuk 2 dimensi dan tidak mempunyai ruang.
Nah, bagi anda yang ingin mempelajari bangun ruang, pada artikel ini
kita akan mencoba membahasnya dengan lebih lengkap.
Seperti yang dijelaskan di atas bahwa bangun ruang ciri utamanya ialah memiliki ruang dan atau volume. Bangun ruang sendiri memiliki berbagai macam bentuk, yakni balok, kubus, kerucut, prisma, tabung, bola dan limas. Setiap bangun ruang tersebut memilikiperhitungan yang berbeda-beda ketika anda akan mencari luas dan juga volumenya.

Rumus Perhitungan Balok
s = panjang rusuk atau sisi kubus
Rumus Perhitungan Limas Segiempat
L = π x r2
Karena bentuknya seperti lingkaran baca juga artikel sebelumnya mengenai luas lingkaran.
Luas selimut
L = 2 x π x r x t
Luas Permukaan
L = 2 x L alas + L selimut = 2 x π x r2 + 2 x π x r x t = 2 x π x r x ( r x t )
Volume Limas Segi Empat
V = π x r2 x t
L = π x r x s
Luas Alas
L alas = π x r2
Luas Permukaan Kerucut
L = L Alas + L Selimut = π x r2 + π x r x s = π r (r + s)
Volume Kerucut
V =1/3 x L alas x Tinggi = 1/3 x π x r2 x t
L = 2 x Luas Alas + Keliling Alas x t
Volume Prisma
V = Luas alas x t
Materi Dimensi Tiga mencakup tentang jarak, sudut pada bangun ruang.
Untuk itulah kita wajib tau tiap bangun ruang . Target kita yang pertama adalah Kubus . Pasti dengar namanya saja udah bisa membayangkan bentuknya kan…???!!
Nah, mari kita kupas tentang sifat-sifat si Kubus ini !
KUBUS ABCD.EFGH

Dalam kubus ABCD.EFGH terdapat :
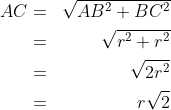
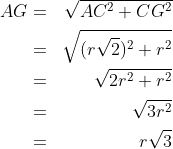 Kita rangkum Rumus Kubus dengan rusuk = r
Kita rangkum Rumus Kubus dengan rusuk = r
Contoh soal :
1. Jika diketahui kubus dengan diagonal sisinya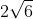 cm , tentukan diagonal ruang kubus !
cm , tentukan diagonal ruang kubus !
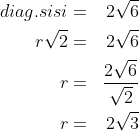
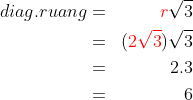
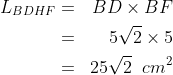
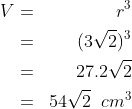
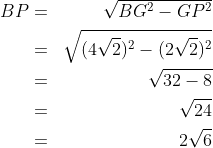
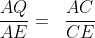
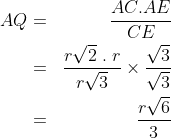
Seperti yang dijelaskan di atas bahwa bangun ruang ciri utamanya ialah memiliki ruang dan atau volume. Bangun ruang sendiri memiliki berbagai macam bentuk, yakni balok, kubus, kerucut, prisma, tabung, bola dan limas. Setiap bangun ruang tersebut memilikiperhitungan yang berbeda-beda ketika anda akan mencari luas dan juga volumenya.
Rumus Bangun Ruang Lengkap

1. Rumus dan Ciri Balok
Balok merupakan sebuah bangun ruang yang memiliki 6 bidang yang memiliki bentuk persegi panjang. Berikut adalah beberapa ketentuan atau ciri-ciri balok.- Memiliki 6 buah sisi dan berbentuk 4 persegi panjang
- Memiliki 12 rusuk, yang dibagi menjadi 3 kelompok, setiap kelompok terdiri atas 4 buah rusuk yang memiliki panjang yang sama.
- Luas sisi yang berhadapan adalah sama, sisi-sisi tersebut terdiri dari 3 bagian yang saling berhadapan
- Semuanya sudutnya siku-siku atau memiliki nilai900
Volume Balok
V = p x l x t
Luas Permukaan Balok
L = 2 x { ( p x l ) + ( p x t ) + ( l x t ) }
Keliling Balok
K = 4 x (p + l + t)
Keterangan:- p = panjang
- l= lebar
- t = tinggi
2. Rumus dan Ciri Kubus
Kubus adalah bangun ruang yang terdiri atas 6 sisi yang mempunyai bentuk bujur sangkar. Ciri-ciri kubus adalah sebagai berikut.- Memiliki 6 sisi yang memiliki luas yang sama
- Bentuknya persegi
- Memiliki 12 rusuk yang memiliki panjang yang sama
- Setiap sudutnya siku-siku (900
Rumus Perhitungan Kubus
Rumus Volume Kubus
V = s x s x s = a3
Luas Permukaan Kubus
L Permukaan = 6 x s x s = 6 x s2
Keliling kubus
K = 12 x s
Keterangan :s = panjang rusuk atau sisi kubus
3. Rumus dan Ciri Bola
Tentunya anda sudah tidak asing lagi dengan bangun ruang bola ini. Berikut beberapa ketentuan bangun ruang dinamakan bola.- Bundar dan merata kesemua arah
- Memiliki jari-jari yang sama panjangnya dari titip tengah (titik pusat) ke semua arah
- Apabila dibelah menjadi dua yang mana melewati titik pusat maka memiliki garis tengah 2 x panjang jari-jari
Rumus Perhitungan Bola
Volume Bola
V = 4/3 x π x r3
Luas Permukaan
L = 4 x π x r2
Keterangan :- r = jari-jari
- π = 22/7 atau 3,14
4. Rumus dan Ciri Limas
Bangun ruang ini juga terdiri atas berbagai macam bentuk. Perbedaan yang sangat mencolok dari bentuk satu dengan yang lainnya adalah terletak pada alasnya, ada yang mempunyai alas segi lima, segi empat dan juga segitiga dan masih banyak lagi. Namun alas limas ini hanya memiliki sifat segi tidak berebntuk bundar. Jika alasnya berbentuk bundar maka disebut dengan nama kerucut.Rumus Perhitungan Limas Segiempat
Luas Alas
L a = sisi x sisi
Luas Sisi Δ
Luas Sisi Δ = 1/2 x a x t
Volume :
V = 1/3 x L alas x t
Luas Permukaan Limas
LP = { ( p + l ) x t) + ( p x l )
5. Rumus dan Ciri Tabung
Seperti halnya bola, tabung ini juga sudah
tidak asing lagi, seringkali kita liat dalam kehidupan sehari-hari.
Seperti drum, kaleng dan lain sebagainya. Tabung ini mempunyai alas dan
juga atas yang mana bentuknya adalah lingkaran. Nah berikut rumus
perhitungannya
Rumus Tabung
Luas AlasL = π x r2
Karena bentuknya seperti lingkaran baca juga artikel sebelumnya mengenai luas lingkaran.
Luas selimut
L = 2 x π x r x t
Luas Permukaan
L = 2 x L alas + L selimut = 2 x π x r2 + 2 x π x r x t = 2 x π x r x ( r x t )
Volume Limas Segi Empat
V = π x r2 x t
6. Rumus dan Ciri Kerucut
Seperti layaknya tabung, kerucut juga
memiliki alas yang berbentuk lingkaran namun kerucut tidak memiliki
penutup atas. Berikut ini adalah rumus bangun ruang kerucut.
Rumus Perhitungan Kerucut
Luas selimutL = π x r x s
Luas Alas
L alas = π x r2
Luas Permukaan Kerucut
L = L Alas + L Selimut = π x r2 + π x r x s = π r (r + s)
Volume Kerucut
V =1/3 x L alas x Tinggi = 1/3 x π x r2 x t
7. Rumus dan Ciri Prisma Tegak Segitiga
Kubus yang memiliki penutup atas dan bawah
segi empat, tabung yang memiliki penutup lingkaran, nah beda lagi dengan
prisma dia memiliki penutup segitiga. Macam-macam aja ya! namun itulah
uniknya bangun ruang.
Rumus Perhitungan Prisma
Luas permukaanL = 2 x Luas Alas + Keliling Alas x t
Volume Prisma
V = Luas alas x t
Materi Dimensi Tiga mencakup tentang jarak, sudut pada bangun ruang.
Untuk itulah kita wajib tau tiap bangun ruang . Target kita yang pertama adalah Kubus . Pasti dengar namanya saja udah bisa membayangkan bentuknya kan…???!!
Nah, mari kita kupas tentang sifat-sifat si Kubus ini !
KUBUS ABCD.EFGH

Dalam kubus ABCD.EFGH terdapat :
- 12 rusuk contoh AB
- 12 diagonal sisi / diagonal bidang contoh EG
- 6 bidang / sisi contoh CDHG
- 6 bidang diagonal contoh ACGE
- 4 diagonal ruang contoh AG
- kita akan cari diagonal sisi AC, perhatikan bidang ABCD (persegi)
- kita akan cari diagonal ruang AG, perhatikan bidang diagonal ACGE (persegi panjang)
- diagonal sisi kubus =
- diagonal ruang kubus =
- Luas permukaan kubus =
- Volume kubus =
Contoh soal :
1. Jika diketahui kubus dengan diagonal sisinya
jawab :
pertama kita cari rusuk nya dulu ya,
maka diagonal ruang kubus
2. Jika diketahui kubus ABCD.EFGH dengan rusuk 5 cm, tentukan luas BDHF !
jawab :
perhatikan BDHF (bidang diagonal) dengan BF = 5 cm (rusuk) dan BD = 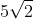 cm (diagonal sisi)
cm (diagonal sisi)
maka luas BDHF
3. Jika diketahui kubus dengan diagonal sisi 6 cm, tentukan Volume kubus tersebut !
jawab :
pertama kita cari rusuknya ya..
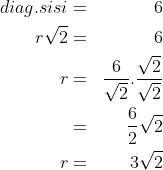
maka volume kubus
Sekarang kita masuk ke contoh soal yang berkaitan dengan jarak dan sudut pada bangun ruang…..yuk
Latihan soal bangun ruang yang berkaitan dengan jarak dan sudut
1. Pada kubus ABCD.EFGH dengan rusuk 4 cm, tentukan jarak titik B ke garis EG !
jawab :
- titik B dan garis EG berada dalam satu bidang yaitu segitiga BEG(sama sisi)
- perhatikan bahwa BE , BG dan EG adalah diagonal sisi sehingga BE = BG = EG =
cm
- proyeksi titik B di garis EG adalah titik P (di tengah EG) sehingga GP =
cm
- jarak yang akan kita cari adalah panjang garis BP
maka :
2. Pada kubus ABCD.EFGH tentukan jarak titik A ke garis CE !
jawab :
- titik A dan garis EC berada dalam satu bidang yaitu segitiga AEC
- perhatikan bahwa AE adalah rusuk, kita misalkan AE = r , sedangkan AC adalah diagonal sisi maka kita misalkan AC =
- proyeksi titik A di garis EC adalah titik Q ( AQ tegak lurus EC)
- jarak yang akan kita cari adalah panjang garis AQ
perhatikan segitiga AQE dan segitiga CAE kita gunakan perbandingan sisi
Logika Matematika
Sebelum kita masuk ke logika matematika, kita harus tahu dulu definisi
logika tersebut yang nantinya sangat berperan dalam pemahaman logika
matematika sendiri. Logika berasal dari kata Yunani kuno λόγος (logos)
yang berarti hasil pertimbangan akal pikiran yang diutarakan lewat kata
dan dinyatakan dalam bahasa. Logika mempunyai beberapa manfaat, yaitu :
1. Pernyataan
Yang dimaksud dengan pernyataan adalah kalimat yang mempunyai nilai benar atau salah tetapi tidak sekaligus kedua-duanya (benar dan salah). Dan suatu kalimat bukan pernyataan jika kita tidak dapat menentukan kalimat tersebut benar atau salah atau mengandung pengertian relatif. Terdapat dua jenis pernyataan matematika yaitu pernyataan tertutup dan pernyataan terbuka. Pernyataan tertutup merupakan pernyataan yang nilai kebenarannya sudah pasti sedangkan pernyataan terbuka yaitu pernyataan yang nilai kebenarannya belum pasti. untuk lebih jelasnya perhatikan contoh dibawah ini.
contoh :
6×5 = 30 ( pernyataan tertutup yang benar )
6+5=10 ( pernyataan tertutup yang salah )
gula putih rasanya manis ( pernyataan terbuka )
Jarak jakarta bandung adalah dekat ( bukan pernyataan, karena dekat itu relatif )
2. Ingkaran Pernyataan ( negasi )
Ingkaran merupakan pernyataan yang menyangkal yang diberikan. Ingkaran pernyataan dapat dibentuk dengan menambah ‘Tidak benar bahwa …’ didepan pernyataan yang diingkar dinotasikan ~.
contoh :
pernyataan B : Sepeda motor beroda dua
negasi pernyataan B : tidak benar sepeda motor beroda dua
3. Pernyataan Majemuk
3.1. Konjungsi
suatu pernyataan p dan q dapat digabung dengan kata hubung ‘dan’ sehingga membentuk pernyataan majemuk ‘ p dan q ‘ yang disebut dengn konjungsi nyang dilambangkan dengan

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi pernyataan majemuk konjungsi.
Jika menemukan suatu pernyataan, kita pasangkan saja dengan tabel disamping sehingga kita dapat menemukan bagaimana kalimat majemuk konjungsinya.

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi kalimat majemuk disjungsi.
sehingga jika kita menemukan suatu pernyataan dan akan kita jadikan kalimat majemuk disjungsi kita tinggal lihat tabel, cari mana yang cocok maka kita akan menemukan bagaimana bentuk kalimat majemuk disjungsinya.
3.3. Implikasi

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi kalimat majemuk implikasi.
sehingga jika kita menemukan suatu pernyataan dan akan kita jadikan kalimat majemuk implikasi kita tinggal lihat tabel disamping, cari mana yang cocok maka kita akan menemukan bagaimana bentuk kalimat majemuk implikasinyanya.
3.4. Biimplikasi
suatu pernyataan p dan q dapat digabung dengan kata hubung ‘jika dan hanya jika’ sehingga membentuk pernyataan majemuk ‘ p jika dan hanya jika q’ yang disebut dengan biimplikasi dan dilambangkan dengan

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi kalimat majemuk biimplikasi.
sehingga jika kita menemukan suatu pernyataan dan akan kita jadikan kalimat majemuk biimplikasi kita tinggal lihat tabel disamping, cari mana yang cocok maka kita akan menemukan bagaimana bentuk kalimat majemuk biimplikasinyanya. Maka kita akan lebih mudah dalam menyelesaikan soal yang nanti akan kita hadapi.
 Ekuivalensi dari pernyataan-pernyataan majemuk ini sangat penting. Kita
harus tahu bentuk negasi dari konjungsi, negasi dari disjungsi dan lain
sebagainya dalam menyelesaikan berbagai bentuk pernyataan yang nantinya
akan muncul. Jadi kita harus hafal bentuk euivalensi
pernyataan-pernyataan majemuk disamping. Maka kita akan lebih mudah
dalam menyelesaikan berbagai tipe soal yang nantinya akan kita temui.
Alangkah baiknya kita hafal ekuivalensi pernyataan-pernyataan disamping.
Ekuivalensi dari pernyataan-pernyataan majemuk ini sangat penting. Kita
harus tahu bentuk negasi dari konjungsi, negasi dari disjungsi dan lain
sebagainya dalam menyelesaikan berbagai bentuk pernyataan yang nantinya
akan muncul. Jadi kita harus hafal bentuk euivalensi
pernyataan-pernyataan majemuk disamping. Maka kita akan lebih mudah
dalam menyelesaikan berbagai tipe soal yang nantinya akan kita temui.
Alangkah baiknya kita hafal ekuivalensi pernyataan-pernyataan disamping.
premis 2 : p ( modus ponens)
__________________
Kesimpulan: q
Arti Modus Ponens adalah “jika diketahui p → q dan p, maka bisa ditarik kesimpulan q“. sebagai contoh :
premis 1 : Jika bapak datang maka adik akan senang
premis 2 : bapak datang
__________________
Kesimpulan: Adik senang
8.2 Modus Tollens
premis 1 : p →q
premis 2 : ~q ( modus tollens)
__________________
Kesimpulan: ~p
Modus Tollens berarti “jika diketahu p → q dan ~q, maka bisa ditarik kesimpulan ~p“. sebagai contoh :
premis 1 : Jika hari hujan, maka adik memakai payung
premis 2 : Adik tidak memakai payung
___________________
Kesimpulan : Hari tidak hujan
8.3 Silogisme
premis 1 : p→q
Silogisme berarti “jika diketahu p → q dan q→r, maka bisa ditarik kesimpulan p→r“. sebagai contoh :
Premis 1 : Jika harga BBM naik, maka harga bahan pokok naik.
Premis 2 : Jika harga bahan pokok naik maka semua orang tidak senang.
__________________________________________________
Kesimpulan: Jika harga BBM naik, maka semua orang tidak senang.
Catatan Tambahan:
Hukum de Morgan:
¬(p Λ q) ≡ (¬p V ¬q)¬(p V q) ≡ (¬p Λ ¬q)
Ekuivalensi implikasi:
(p → q) ≡ (¬p V q)
- Membantu setiap orang yang mempelajari logika untuk berpikir secara rasional, kritis, lurus, tetap, tertib, metodis dan koheren.
- Meningkatkan kemampuan berpikir secara abstrak, cermat, dan objektif.
- Menambah kecerdasan dan meningkatkan kemampuan berpikir secara tajam dan mandiri.
- Memaksa dan mendorong orang untuk berpikir sendiri dengan menggunakan asas-asas sistematis
- Meningkatkan cinta akan kebenaran dan menghindari kesalahan-kesalahan berpkir, kekeliruan, serta kesesatan.
- Mampu melakukan analisis terhadap suatu kejadian.
- Terhindar dari klenik , gugon-tuhon ( bahasa Jawa )
- Apabila sudah mampu berpikir rasional,kritis ,lurus,metodis dan analitis sebagaimana tersebut pada butir pertama maka akan meningkatkan citra diri seseorang.
1. Pernyataan
Yang dimaksud dengan pernyataan adalah kalimat yang mempunyai nilai benar atau salah tetapi tidak sekaligus kedua-duanya (benar dan salah). Dan suatu kalimat bukan pernyataan jika kita tidak dapat menentukan kalimat tersebut benar atau salah atau mengandung pengertian relatif. Terdapat dua jenis pernyataan matematika yaitu pernyataan tertutup dan pernyataan terbuka. Pernyataan tertutup merupakan pernyataan yang nilai kebenarannya sudah pasti sedangkan pernyataan terbuka yaitu pernyataan yang nilai kebenarannya belum pasti. untuk lebih jelasnya perhatikan contoh dibawah ini.
contoh :
6×5 = 30 ( pernyataan tertutup yang benar )
6+5=10 ( pernyataan tertutup yang salah )
gula putih rasanya manis ( pernyataan terbuka )
Jarak jakarta bandung adalah dekat ( bukan pernyataan, karena dekat itu relatif )
2. Ingkaran Pernyataan ( negasi )
Ingkaran merupakan pernyataan yang menyangkal yang diberikan. Ingkaran pernyataan dapat dibentuk dengan menambah ‘Tidak benar bahwa …’ didepan pernyataan yang diingkar dinotasikan ~.
contoh :
pernyataan B : Sepeda motor beroda dua
negasi pernyataan B : tidak benar sepeda motor beroda dua
3. Pernyataan Majemuk
3.1. Konjungsi
suatu pernyataan p dan q dapat digabung dengan kata hubung ‘dan’ sehingga membentuk pernyataan majemuk ‘ p dan q ‘ yang disebut dengn konjungsi nyang dilambangkan dengan

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi pernyataan majemuk konjungsi.
Jika menemukan suatu pernyataan, kita pasangkan saja dengan tabel disamping sehingga kita dapat menemukan bagaimana kalimat majemuk konjungsinya.
3.2. Disjungsi
suatu
pernyataan p dan q dapat digabung dengan kata hubung ‘atau’ sehingga
membentuk pernyataan majemuk ‘ p atau q’ yang disebut dengn disjungsi
yang dilambangkan dengan

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi kalimat majemuk disjungsi.
sehingga jika kita menemukan suatu pernyataan dan akan kita jadikan kalimat majemuk disjungsi kita tinggal lihat tabel, cari mana yang cocok maka kita akan menemukan bagaimana bentuk kalimat majemuk disjungsinya.
3.3. Implikasi
suatu
pernyataan p dan q dapat digabung dengan kata hubung ‘jika maka’
sehingga membentuk pernyataan majemuk ‘ jikap maka q’ yang disebut
dengan implikasi dan dilambangkan dengan

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi kalimat majemuk implikasi.
sehingga jika kita menemukan suatu pernyataan dan akan kita jadikan kalimat majemuk implikasi kita tinggal lihat tabel disamping, cari mana yang cocok maka kita akan menemukan bagaimana bentuk kalimat majemuk implikasinyanya.
3.4. Biimplikasi
suatu pernyataan p dan q dapat digabung dengan kata hubung ‘jika dan hanya jika’ sehingga membentuk pernyataan majemuk ‘ p jika dan hanya jika q’ yang disebut dengan biimplikasi dan dilambangkan dengan

Tabel disamping menunjukan beberapa pernyataan yang digabungkan menjadi kalimat majemuk biimplikasi.
sehingga jika kita menemukan suatu pernyataan dan akan kita jadikan kalimat majemuk biimplikasi kita tinggal lihat tabel disamping, cari mana yang cocok maka kita akan menemukan bagaimana bentuk kalimat majemuk biimplikasinyanya. Maka kita akan lebih mudah dalam menyelesaikan soal yang nanti akan kita hadapi.
4. Ekuivalensi pernyataan-pernyataan majemuk
 Ekuivalensi dari pernyataan-pernyataan majemuk ini sangat penting. Kita
harus tahu bentuk negasi dari konjungsi, negasi dari disjungsi dan lain
sebagainya dalam menyelesaikan berbagai bentuk pernyataan yang nantinya
akan muncul. Jadi kita harus hafal bentuk euivalensi
pernyataan-pernyataan majemuk disamping. Maka kita akan lebih mudah
dalam menyelesaikan berbagai tipe soal yang nantinya akan kita temui.
Alangkah baiknya kita hafal ekuivalensi pernyataan-pernyataan disamping.
Ekuivalensi dari pernyataan-pernyataan majemuk ini sangat penting. Kita
harus tahu bentuk negasi dari konjungsi, negasi dari disjungsi dan lain
sebagainya dalam menyelesaikan berbagai bentuk pernyataan yang nantinya
akan muncul. Jadi kita harus hafal bentuk euivalensi
pernyataan-pernyataan majemuk disamping. Maka kita akan lebih mudah
dalam menyelesaikan berbagai tipe soal yang nantinya akan kita temui.
Alangkah baiknya kita hafal ekuivalensi pernyataan-pernyataan disamping.
Tidak
perlu bingung dan terbebani, kunci dari matematika adalah hafal rumus
dan bisa menggunakannya. Jika kita sering latihan soal maka secara
otomatis kita akan hafal, dan pastinya kita akan mudah menggunakan rumus
tersebut jika diterapkan dalam soal.
5. Konvers, Invers dan Kontraposisi
Dari sebuah implikasi dapat diturunkan pernyataan yang disebut konvers, invers dan kontraposisi dari implikasi tersebut
6. Pernyataan Berkuantor
Pernyataan berkuantor merupakan pernyataan yang mengandung ukuran kuantitas. Ada 2 macam yaitu :
6.1 Kuantor Universal
Dalam
pernyataan kuantor universal terdapat ungkapan yang menyatakan semua,
setiap. Kuantor universal dilambangkan dengan ∀(dibaca untuk semua atau
untuk setiap).
contoh : ∀ x  R, x>0 dibaca untuk setiap x anggota bilangan riil maka berlaku x>0.
R, x>0 dibaca untuk setiap x anggota bilangan riil maka berlaku x>0.
6.2 Kuantor Eksistensial
Dalam
pernyataan kuantor eksistensial terdapat ungkapan yang menyatakan ada,
beberapa, sebagian, terdapat. Kuantor eksistensial dilambangkan dengan ∃
( dibaca ada, beberapa, terdapat, sebagian )
contoh : ∀ x  R, x+5>1 dibaca terdapat x anggota bilangan riil dimana x+5>1.
R, x+5>1 dibaca terdapat x anggota bilangan riil dimana x+5>1.
7. Ingkaran dari pernyataan berkuantor
Ingkaran
dari pernyataan berkuantor universal adalah pernyataan berkuantor
eksistensial, begitu juga sebaliknya ingkaran dari pernyataan berkuantor
eksistensial adalah pernyataan berkuantor universal.
contoh :
p : beberapa siswa SMA rajin belajar
~p : semua siswa SMA tidak rajin belajar
8. Penarikan Kesimpulan
Penarika
kesimpulan dilakukan dari beberapa pernyataan yang diketahui nilai
kebenarannya yang disebut premis. Kemudian dengan menggunakan
prinsip-prinsip yang ada diperoleh pernyataan yang baru yang disebut
kesimpulan/konklusi yang diturunkan dari premis yang ada. Penarikan
kesimpulan seperti itu sering disebut dengan argumentasi. Suatu
argumentasi dikatakan sah Jika premis-premisnya benar maka konklusinya
juga benar. Terdapat 3 metode dalam penarikan kesimpulan, yaitu :
8.1 Modus ponens
premis 1 : p →qpremis 2 : p ( modus ponens)
__________________
Kesimpulan: q
Arti Modus Ponens adalah “jika diketahui p → q dan p, maka bisa ditarik kesimpulan q“. sebagai contoh :
premis 1 : Jika bapak datang maka adik akan senang
premis 2 : bapak datang
__________________
Kesimpulan: Adik senang
8.2 Modus Tollens
premis 1 : p →q
premis 2 : ~q ( modus tollens)
__________________
Kesimpulan: ~p
Modus Tollens berarti “jika diketahu p → q dan ~q, maka bisa ditarik kesimpulan ~p“. sebagai contoh :
premis 1 : Jika hari hujan, maka adik memakai payung
premis 2 : Adik tidak memakai payung
___________________
Kesimpulan : Hari tidak hujan
8.3 Silogisme
premis 1 : p→q
premis 2 : q → r ( silogisme)
_________________
Kesimpulan: p →rSilogisme berarti “jika diketahu p → q dan q→r, maka bisa ditarik kesimpulan p→r“. sebagai contoh :
Premis 1 : Jika harga BBM naik, maka harga bahan pokok naik.
Premis 2 : Jika harga bahan pokok naik maka semua orang tidak senang.
__________________________________________________
Kesimpulan: Jika harga BBM naik, maka semua orang tidak senang.
Catatan Tambahan:
Hukum de Morgan:
¬(p Λ q) ≡ (¬p V ¬q)¬(p V q) ≡ (¬p Λ ¬q)
Ekuivalensi implikasi:
(p → q) ≡ (¬p V q)
10 Fakta Unik Tentang Mesut Ozil
 Mesut Ozil.
LONDON – Arsenal memang telah resmi mendatangkan Mesut Ozil dari Real Madrid, bahkan The Gunners rela merogoh kocek dalam-dalam demi mendapatkan tanda tangan pemain internasional Jerman itu.
Mesut Ozil.
LONDON – Arsenal memang telah resmi mendatangkan Mesut Ozil dari Real Madrid, bahkan The Gunners rela merogoh kocek dalam-dalam demi mendapatkan tanda tangan pemain internasional Jerman itu.Atas keberhasilan Arsene Wenger merekrut Ozil, ternyata banyak fakta menarik tentang mantan pemain Werder Bremen tersebut. Mulai dari saat dirinya lahir, hingga resminya Ozil berseragam Meriam London.
Berikut ini 10 fakta menarik tentang Ozil, seperti dilansir Bleacher Report:
1. Dia Merupakan Pemain Paling Kreatif di Sepakbola Eropa
Berdasarkan dari situs resmi Ozil, pemain 24 tahun itu telah memainkan 353 pertandingan resmi baik untuk klub, maupun Timnas Jerman. Sisi menariknya adalah, Ozil telah membuat 12.647 passing (85 persen sukses), mencetak 59 gol dan yang paling penting dia menciptakan 122 assist.
2. Teknik Bola yang Indah
Para pencita sepakbola Eropa bisa membuktikan fakta bahwa Mesut Ozil merupakan pemain yang menarik untuk ditonton di lapangan. Terlepas dari bayang-bayang Cristiano Ronaldo, Ozil sering memamerkan kualitasnya secara konsisten dengan penguasaan bola yang baik. Visi ‘mata elang’ dan gol-gol yang dicetak berguna dari waktu ke waktu.
Ozil juga menjadi ancaman bagi penjaga gawang lawan, karena memiliki tendangan jarak jauh yang akurat. Bahkan, secara luas banyak pengamat sepakbola bahwa dia sekarang ini sering dibanding-bandingkan dengan Lionel Messi, Zinedine Zidane, dan Luis Figo.
3. Memiliki Darah Turki
Anda mungkin enggak perlu berbicara atau belajar bahasa Jerman untuk mengetahui kalau Mesut Ozil bukan nama asli bangsa itu. Dia adalah generasi ketiga Turki-Jerman yang merupakan keturunan kurdi. Ozil lahir di kota pertambangan Ruhr, Gelsenkirchen di mana dia menghabiskan masa kecilnya di Schalke 04.
Ayah Ozil bernama Mustafa Ozil, pindah ke Jerman pada saat berusia dua tahun dan nenek moyangnya berasal dari sebuah kota di Utara Turki yang disebut Derek. Uniknya kota ini bercuaca dingin selama musim panas, dan memilki cuaca hangat di saat memasuki musim dingin.
4.Sempat Dijuluki “der Neue Diego”
Diego Ribas da Cunha adalah gelandang serang Brasil yang sempat menghujani jendela transfer dengan dikaitkan beberapa klub besar Eropa, sebelum akhirnya kini menetap di VFL Wolfsburg.
Mendarat di Eropa, Diego memilih FC Porto, sebagai suksesor Deco yang hengkang ke Barcelona. Kemudian Diego bergabung bersama Werder Bremen dan membantu klubnya meraih DFB Pokal pada musim 2009. Setelah bermain apik, dia kemudian pergi ke Juventus, namun sayang dia meredup bersama Nyonya Tua.
Sementara Mesut Ozil tiba di Bremen dan akrab dipanggil “der Neue Diego” (Diego Berikutnya). Seperti Diego, Ozil diprioritaskan bermain di belakang stiker. Ozil pun mengukir namanya dengan mencetak gol untuk kemenangan Bremen menjuarai DFB Pokal dan membantu membawa Bremen tampil di Final Piala UEFA.
5. Roda Penggerak di Timnas Jerman
Meski berdarah Turki, namun Ozil lebih memilih untuk memperkuat Timnas Jerman Senior dan melakukan debutnya pada Februari 2009. Di Piala Dunia 2010 penampilannya sangat menonjol di fase grup, hingga membawa Tim Panser mencapai peringkat ketiga, usai mengalahkan Uruguay.
Penampilan apik Ozil berlanjut ke kualifikasi Euro 2012, dia menciptakan tujuh assist untuk rekan setimnya, yang membuatnya dinobatkan sebagai pemain paling kreatif selama kualifikasi. Dengan segala pencapaiannya di Timnas Jerman, Ozil layak dijadikan roda penggerak yang akan mengancam tim lawan di Piala Dunia 2014.
Trigonometri
Trigonometri merupakan cabang ilmu matematika yang mempelajari tentang garis dan sudut suatu segitiga.
Hubungan antara garis dan sudut ini lah yang akan menjadi fungsi-fungsi trigonometri.
Berikut ini adalah fungsi dasarnya (sinus, cosinus, tangen):
Pada segitiga ABC di samping, dengan panjang AB adalah q, BC = p, dan AC = r, serta sudut CAB = X, maka berlaku:
 ,
,  ,
, 
Kemudian ,
,  ,
, 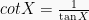
 Pada sudut istimewa, yaitu
Pada sudut istimewa, yaitu  dan kelipatannya, nilai sinus, cosinus, dan tangennya berupa bilangan sederhana, seperti pada tabel di samping.
dan kelipatannya, nilai sinus, cosinus, dan tangennya berupa bilangan sederhana, seperti pada tabel di samping.
Sedangkan nilai sec, cosec, dan cot dapat diperoleh dengan menggunakan hubungannya dengan sin, cos, dan tan di atas.
Nilai sin, cos, dan tan sudut istimewa ini harus hafal, karena akan selalu digunakan untuk materi lainnya seperti integral, limit, dll.
Contoh soal:
Pada segitiga siku-siku ABC dengan sisi miring BC dan sisi tegak AB, panjang BC = 5cm, dan panjang AB = 4cm, tentukanlah nilai dari cos C.
Jawaban:
Cos C = AC/BC. Panjang AB dan BC sudah diketahui, tetapi panjang AC belum harus kita cari terlebih dahulu.
Karena segitiga tersebut siku-siku, maka dapat digunakan dalil pythagoras, yaitu AC^2 = BC^2 – AB^2 = 5^2 – 4^2 = 9. Jadi panjang AC = 3cm
Oleh karena itu,
Note: Untuk sudut istimewa kelipatannya, seperti dan sebagainya, dapat diperoleh dengan menggunakan sifat jumlah dan selisih sudut.
dan sebagainya, dapat diperoleh dengan menggunakan sifat jumlah dan selisih sudut.
Hubungan antara garis dan sudut ini lah yang akan menjadi fungsi-fungsi trigonometri.
Berikut ini adalah fungsi dasarnya (sinus, cosinus, tangen):

Pada segitiga ABC di samping, dengan panjang AB adalah q, BC = p, dan AC = r, serta sudut CAB = X, maka berlaku:
Kemudian
Trigonometri Untuk Sudut Istimewa
 Pada sudut istimewa, yaitu
Pada sudut istimewa, yaitu Sedangkan nilai sec, cosec, dan cot dapat diperoleh dengan menggunakan hubungannya dengan sin, cos, dan tan di atas.
Nilai sin, cos, dan tan sudut istimewa ini harus hafal, karena akan selalu digunakan untuk materi lainnya seperti integral, limit, dll.
Contoh soal:
Pada segitiga siku-siku ABC dengan sisi miring BC dan sisi tegak AB, panjang BC = 5cm, dan panjang AB = 4cm, tentukanlah nilai dari cos C.
Jawaban:
Cos C = AC/BC. Panjang AB dan BC sudah diketahui, tetapi panjang AC belum harus kita cari terlebih dahulu.
Karena segitiga tersebut siku-siku, maka dapat digunakan dalil pythagoras, yaitu AC^2 = BC^2 – AB^2 = 5^2 – 4^2 = 9. Jadi panjang AC = 3cm
Oleh karena itu,
Note: Untuk sudut istimewa kelipatannya, seperti
10 Fakta Unik Tentang Indonesia
Negara Indonesia adalah
negara yang sangat khas dan juga unik. Banyak hal-hal tentang Indonesia
yang sangat unik dan mungkin hanya bisa dijumpai di negara Indonesia
ini serta tidak akan ditemui di negara-negara yang lainnya. Namun
sayangnya, tidak semua hal unik di Indonesia itu bersifat positif,
karena ada juga beberapa hal-hal unik tentang negara Indonesia yang juga
bersifat negatif.
Ya, beberapa
hal unik di Indonesia memang bersifat negatif yang ironisnya sudah
melekat dalam kebudayaan Indonesia. Namun juga ada beberapa hal unik
lain yang mungkin belum banyak diketahui oleh masyarakat Indonesia.
Langsung saja, berikut 10 Fakta Unik tentang Indonesia yang mungkin tidak atau belum anda ketahui :
1. Negara Maritim Terbesar di Dunia
Indonesia juga
dikenal sebagai negara maritim terbesar di dunia. Total perairan di
Indonesia seluas lebih dari 3,2 juta km2 dan juga memiliki garis pantai
terpanjang kedua di dunia setelah negara Kanada. Untuk mengamankannya
dari serangan musuh dan pencuri kekayaan alam di Indonesia, tentu
dibutuhkan pasukan militer yang tangguh. Dan untuk tugas itu diserahkan
kepada marinir angkatan laut Indonesia.
2. Memiliki Presiden Terkorup Sedunia
Negara
Indonesia sudah dikenal sebagai negara yang korup sejak dulu. Bahkan,
presiden kedua Indonesia, Soeharto mencatat 'prestasi' sebagai pemimpin
negara paling korup sedunia. Selama 32 tahun masa pemerintahannya,
Soeharto diperkirakan melakukan korupsi sebesar 15 hingga 35 milyar
dollar AS. Prestasi ini dicapai Soeharto selama 32 tahun masa
pemerintahannya. Namun meski akhirnya pada 1998 Soeharto turun jabatan
dan akhirnya meninggal dunia, Soeharto belum sempat diadili karena
berbagai hambatan.
3. Nama-Nama Presiden yang Tidak Dikenal
Hingga tahun
2013, Indonesia telah memiliki 6 presiden. Mereka adalah Soekarno,
Soeharto, Habibie, Gus Dur, Megawati, dan yang terakhir Susilo Bambang
Yudhoyono alias SBY. Namun, ada dua nama yang terlewat, yakni Sjafruddin
Prawiranegara dan Mr Assaat.
Faktanya, kedua
nama tersebut pernah menjabat sebagai kepala negara di Indonesia.
Sjafrudin Prawiranegara pernah ditugaskan sebagai Presiden atau Ketua
PDRI (Pemerintah Darurat Republik Indonesia) pada tahun 1948 untuk
menjalankan roda pemerintahan dari Bukittinggi. Hal itu disebabkan
karena saat itu presiden dan wakil presiden, Soekarno dan Hatta
ditangkap Belanda pada Agresi Militer II. Sedangkan untuk kasus
Mr.Assaat lain lagi. Ia sempat memangku jabatan menjadi presiden
sementara sejak bulan Desember 1949 hingga bulan Agustus 1950.
4. Kuburan Aneh di Indonesia
Ada banyak cara
menguburkan jenazah, dan orang Indonesia punya cara yang unik dalam
melakukannya. Orang-orang dari suku Toraja di Sulawesi Selatan
memakamkan jenazah di bukit atau tebing-tebing yang terjal. Sedangkan
suku Dayak di pedalaman Kalimantan Timur juga punya kuburan unik. Mayat
tidak dikubur di dalam tanah, melainkan diletakkan ke dalam peti yang
disangga oleh tiang atau digantung pada tali. Setelah beberapa tahun
peti itu dibuka lagi, lalu tulang-belulang mayat didoakan, kemudian
dimasukkan lagi ke dalam peti bertiang yang permanen. Kemudian ada juga
makam Batu Karang Terjal Londa, dimana mayat akan dimasukkan ke
peti-peti yang kemudian diatur sesuai garis keturunan keluarga, lalu
diletakkan di dalam goa yang dalamnya sekitar seribu meter.
5. Pemimpin yang Cacat Fisik
Indonesia juga
tercatat sebagai satu-satunya negara yang memiliki presiden yang cacat
fisik. Pada tahun 1999, KH. Abdurrahman Wahid alias Gus Dur resmi
menjadi Presiden Republik Indonesia ke-4. Gus Dur menderita gangguan
penglihatan hingga seringkali orang lain yang membacakan atau menuliskan
surat untuknya. Selain itu Gus Dur juga menderita diabetes, gangguan
ginjal, bahkan beberapa kali terserang stroke. Namun segala keterbatasan
fisik tersebut tidak menghalanginya untuk menjadi pemimpin negara. Ia
dikenang sebagai pahlawan kebebasan, pembela kaum minoritas dan pejuang
HAM.
6. Nama Jalan Pahlawan Indonesia di Belanda
Indonesia dan
Belanda punya hubungan sejarah yang dekat. Oleh karena itu banyak unsur
budaya kedua negara yang berbaur. Dan jika kita berjalan-jalan ke
Belanda, maka akan ditemukan nama-nama jalan yang diambil dari nama
pahlawan perjuangan Indonesia di beberapa kota. Ada nama jalan Mohammed
Hatta dan Sutan Sjahrir di kota Haarlem, dan jalan RA Kartini yang ada
di empat kota sekaligus di Belanda, yaitu di Amsterdam, Haarlem,
Utrecht, dan Venlo.
7. Orang Terkenal Keturunan Indonesia
Sedikit orang
Indonesia yang bisa terkenal hingga ke luar negeri, bahkan mungkin
hampir tak ada. Namun ada beberapa orang keturunan Indonesia yang sukses
di luar negeri yang kebanyakan dari negeri Belanda karena sisi historis
kedua negara yang begitu dekat. Sebagai contoh di timnas sepakbola
Belanda, ada banyak pemain keturunan Indonesia. Mulai dari Robin Van
Persie, John Heitinga, Nigel de Jong, Denny Landzaat, Demy De Zeeuw, dan
Giovanni van Bronckhorst. Selain itu juga ada pemain keturunan Batak,
Radja Nainggolan asal Belgia.
Singapura juga
pernah punya Perdana Menteri keturunan Indonesia, yakni Lee Kuan Yew
yang berdarah Semarang dan Pontianak dari kedua neneknya. Bahkan
presiden pertama Singapura, Yusof Ishak, yang wajahnya diabadikan dalam
pecahan uang kertas Singapura, merupakan keturunan Minangkabau, Sumatera
Barat.
8. Negara Republik pertama sebelum Indonesia
Jauh sebelum
negara republik Indonesia ada, sudah ada sebuah negara republik yang
pernah berdiri di tanah Indonesia. Dua abad yang lalu, sebuah negara
bernama Republik Lan Fang pernah berdiri di kota Pontianak, Kalimantan
Barat. Saat itu bangsa Eropa dan Cina yang lebih maju sejarah
peradabannya pun masih memakai sistem Kerajaan dan Monarki. Pejabat
tinggi dari Lan Fang berpakaian ala Cina kuno. Republik Lan Fang
akhirnya takluk di tangan penjajah Belanda.
9. Arti Sebuah Nama Bagi Soekarno
Jika Presiden
Soekarno bisa memutar balik waktu, mungkin ia akan mengubah nama
tandatangannya pada naskah Proklamasi. Saat sudah menjabat sebagai
Presiden, Soekarno mengubah penulisan namanya dari Soekarno menjadi
Sukarno. Hal ini dikarenakan Soekarno sangat membenci ejaan “oe” yang
dianggapnya warisan penjajah Belanda. Sayangnya, naskah Proklamasi tidak
boleh dirubah sama sekali.
Soekarno
sendiri dilahirkan dengan nama Kusno Sosrodihardjo, sebelum dirubah
ayahnya menjadi Soekarno karena sering sakit-sakitan saat kecil dulu.
Terbukti saat menyandang nama Soekarno ia jadi makin berjaya. Namun
ketika ia merubah lagi namanya menjadi Sukarno, nasibnya menjadi buruk
lagi.
10. Tetangga yang Baik Bagi Malaysia
Indonesia juga
menjadi negara tetangga yang baik bagi Malaysia. Sudah beberapa kali
Malaysia mencuri dan mengklaim budaya-budaya di Indonesia serta
pulau-pulau terluarnya. Namun pemerintah Indonesia justru tidak
melakukan tindakan dan cenderung membiarkannya. Oleh karena itu, hal-hal
seperti pencurian ikan, pencurian pasir, illegal logging, dan
sebagainya dari pihak asing tidak pernah diproses hukum.
Langganan:
Komentar (Atom)





